Neueste Erkenntnisse, inspirierende Geschichten und praktische Insights zu den wichtigsten Themen rund um Softwareentwicklung, Agile Methoden und Business Transformation – präsentiert von unseren iteratec-Expert*innen.

Wenn ich als Security-Berater in Projekte komme und nach dem Threat Model frage, ist die Antwort häufig: „Haben wir eingeplant!...
Tags: Security

Many leaders have high expectations when starting an agile transformation. Just imitating what, e.g. the Scrum Guide describes,...
Tags: Agility

Den Arbeitsalltag von Handwerker:innen einfacher und produktiver machen: Das ist der Auftrag von Festool. Das Familienunternehmen...
Tags: Innovation, Künstliche Intelligenz

Agile has exceeded the boundaries of it’s original domain, software development. Today many companies claim to do Agile. Projects...
Tags: Agility

Fehlendes technisches Know-how und fehlende personelle Ressourcen – sie gehören zu den Top-Gründen, die Unternehmen beim Einsatz...

When people feel they have no influence on the organizations goals, they become disconnected from the products they build and...
Tags: Agility

Machine-Learning-Expert:innen bei iteratec haben für das interne Marketing-Team einen Text- und Bild-Generator entwickelt. Damit...
Tags: Technology, Artificial Intelligence, Innovation,

Wir haben eine bewährte Best-Practice-Architektur entwickelt, die sich bei vielen Kunden als effektiv für die Anforderungen...
Tags: Software, Infrastructure, Technology,

Die Motivation vieler Unternehmen, in die Cloud zu migrieren, ist die Effizienz ihrer IT zu steigern und Kosten zu senken. Doch...
Tags: Infrastructure, Technology, People

Beim Einsatz moderner Cloud-Technologien ist eine maßgeschneiderte Plattformstrategie für die effiziente und einheitliche...
Tags: Software, Technology

Heute feiern wir nicht nur den Weltfrauentag, sondern auch das zweite Jahr unseres Frauennetzwerks women@iteratec. Zu diesem...
Tags: People

„Wo stand das noch mal?“ Wer als Mitarbeitender nach internen Dokumenten sucht, stellt sich diese Frage häufiger. Jeden Tag...

E-Mail-Phishing ist als gängige Angriffstaktik bekannt. Es wird aber oft vergessen, dass andere Kollaborationsplattformen genauso...
Tags: Security, Infrastructure, Technology,

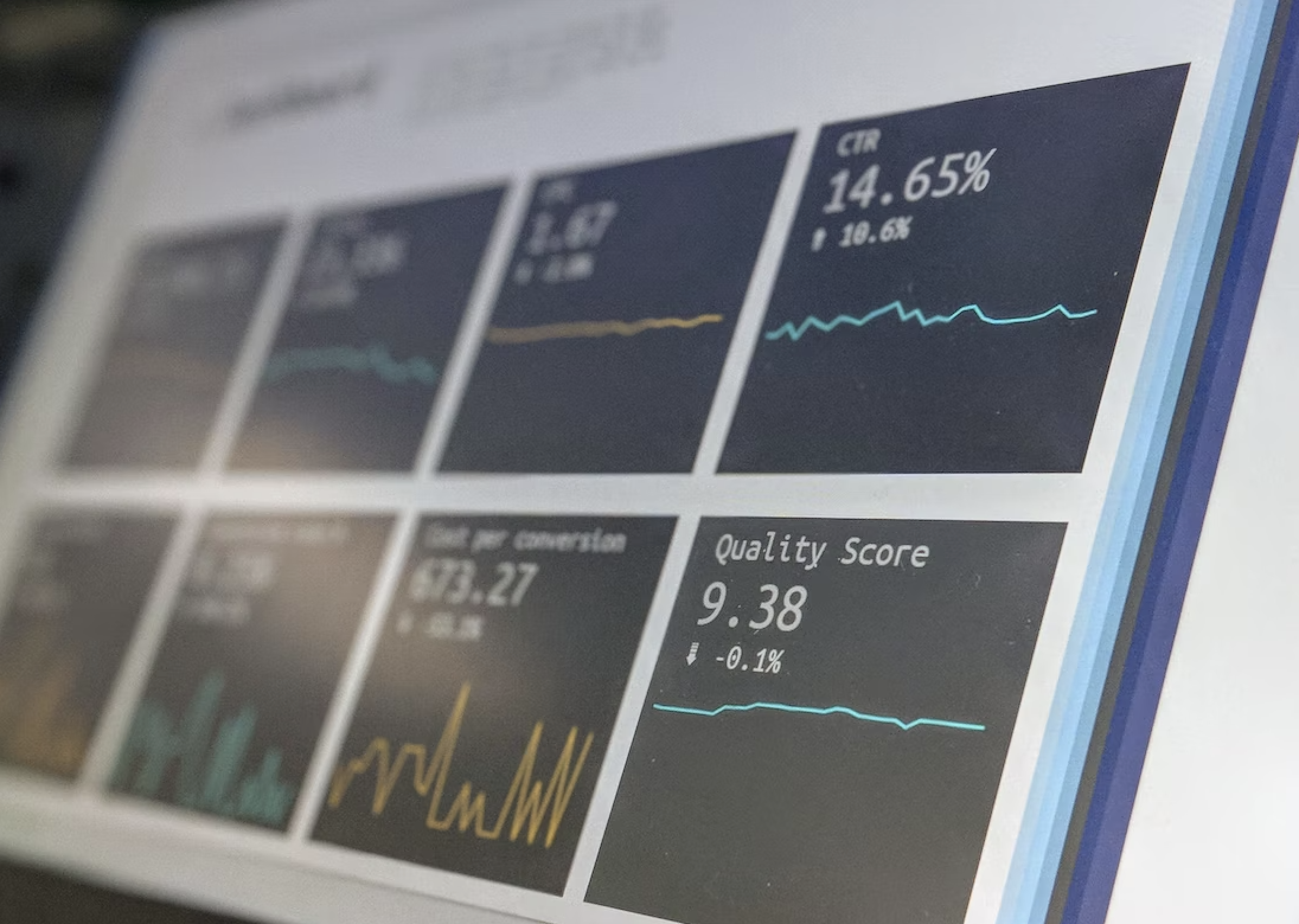
In der industriellen Fertigung ist die visuelle Qualitätskontrolle ein äußerst wichtiger Prozess, um beispielsweise...
Tags: Technology, Artificial Intelligence, Data,

Are you looking for effective ways to secure your Spring applications? Look no further! Our very own Dr. Ing. Max Maass has...
Tags: Software, Technology

In einer Welt, in der künstliche Intelligenz (AI) immer mehr an Bedeutung gewinnt, ist es entscheidend, die Sicherheit und...
Tags: Software, Security, Infrastructure,

Metaframeworks wie Next.js, SvelteKit oder Astro sind zurzeit in aller Munde. Diese übernehmen gewisse Aufgaben rund um...
Tags: Software, Technology

Anfang des Jahres haben wir die auf Digital Business Innovation spezialisierte Agentur HI NEXT übernommen. Chris Ehl war...
Tags: Innovation, Digital Business, People

Are you looking for effective ways to secure your Spring applications? Look no further! Our very own Dr. Ing. Max Maass has...
Tags: Software, Technology

Are you looking for effective ways to secure your Spring applications? Look no further! Our very own Dr. Ing. Max Maass has...
Tags: Software, Technology

Generative Artificial Intelligence (GenAI) ist eine fortschrittliche Form der künstlichen Intelligenz: Sie simuliert...
Tags: Artificial Intelligence, Innovation, Digital Business,

Während die Entwicklungen im Bereich der künstlichen Intelligenz (KI), besonders bei Generativer KI, immer weiter fortschreiten,...

![Book[it]: Ein Studierenden-Projekt, das Raumbuchungen erleichtert.](https://explore.iteratec.com/hubfs/Armin_Ganic_Mitarbeiterfoto-1.png)
Technologie muss man ausprobieren, um sie zu beherrschen. Den nötigen Freiraum dafür schaffen wir u. a. mit unserem...
Tags: Software, Technology, Innovation

Geschichten über erfolgreiche Unternehmer:innen und ihre Karrierewege sind häufig inspirierend und ermutigend. Im Podcast „Meet a...
Tags: New Work, Digital Business, People

Anfang 2023 hat ein Technologiesprung im Bereich der Künstlichen Intelligenz (KI) stattgefunden. Dieser wurde insbesondere durch...

Die einzelnen Bausteine im Web3 wie zum Beispiel digitale Fashion-NFTs, Token Gates, Loyalty Programme oder auch...
Tags: Blockchain, Web3

Musik mit Künstlicher Intelligenz (KI) produzieren ist kein futuristisches Konzept mehr. Tools wie AIVA und MusicLM von Google...

Die vielfältigen Elemente von Web3, wie digitale Fashion-NFTs, Token Gates, Loyalitätsprogramme und Blockchain-basierte...
Tags: Blockchain, Web3

„Intelligente“ Software-Systeme, die Antworten auf nahezu alle Fragen parat haben, Texte zusammenfassen können, gleichzeitig als...
Tags: Artificial Intelligence, Data

Die Pandemie hat gezeigt, dass die Digitalisierung notwendig ist, um bestehende Geschäftsmodelle zu erhalten. Darüber hinaus...
Tags: Blockchain, Web3

Im Web3 entstehen mehr und mehr Chancen für Creator, ihre Werke direkt an die Endkonsumenten zu verkaufen. Die Creator Economy...
Tags: Web3

Durch den Einsatz von Blockchain und NFTs ergeben sich für Marken neue Möglichkeiten im Metaverse, die Customer Relations in den...
Tags: Blockchain, Web3

Die iteratec nurdemteam eG ist Gesellschafterin der iteratec GmbH. Sophia Breth ist auf der letzten Generalversammlung mit 85%...
Tags: People

Mit der fortschreitenden Verschmelzung von digitalen und physischen Räumen erleben wir eine Ausdehnung des sozialen Raums. Aus...
Tags: Web3

MultiJuicer is an official part of the Juice Shop OWASP project and the official multi user platform for Juice Shop since end of...
Tags: Security, Technology

Künstliche Intelligenz und generative Sprachmodelle sind hier, um zu bleiben. Das zeigt auch die Frequenz mit der neue...
Tags: Technology, Artificial Intelligence, Innovation,

Die Cloud verändert, wie Unternehmen ihre IT-Infrastruktur bereitstellen und betreiben. Auf der einen Seite können Unternehmen...
Tags: Infrastructure, Technology

Machine Learning kann nur bei großen Datenmengen zum Einsatz kommen - oder?
Tags: Artificial Intelligence, Innovation, Data

Fabian ist seit 2022 DevOps Engineer bei iteratec. Er hat einen Master in Physik der Atmosphäre/Meteorologie und arbeitete in...
Tags: People

Im zweiten Teil der Blogartikelreihe rund um das Thema Erfolgsfaktor Chatbots widmen wir uns der Fragestellung, wie Sie Ihre...
Tags: Artificial Intelligence, Innovation, Data

Tags: Artificial Intelligence, Innovation, Data
Tags: Artificial Intelligence, Data

Tags: Blockchain, Web3

Tags: Artificial Intelligence, Data

Tags: Software

Tags: Blockchain, Web3

Seit etwas über dreieinhalb Jahren arbeitet Tehseen bei iteratec. Zuvor absolvierte er ein Studium in theoretischer und...
Tags: People

Poking around in the world of NFTs you will primarily come into contact with NFTs on Ethereum Virtual Machine (EVM) based...
Tags: Blockchain

Poking around in the world of NFTs you will primarily come into contact with NFTs on Ethereum Virtual Machine (EVM) based...
Tags: Blockchain

Wer bei NFTs nur an Bilder von gelangweilten Affen oder an spekulationsreiche Kunstobjekte denkt, der übersieht das Potenzial der...
Tags: Innovation, Digital Business, Blockchain,

Tags: Software, Security, Infrastructure

Serverless eröffnet riesige Potenziale für die Frontend-Entwicklung. Als Fullstack-Entwickler berichtet unser Autor Jannik an...
Tags: Software, Technology

Im Fahrzeug ist die Medizin längst angekommen: Tritt dort ein Defekt auf, werden Diagnosesysteme eingesetzt, um mögliche Ursachen...
Tags: Technology, Innovation, Architecture

Serverless eröffnet riesige Potenziale für die Frontend-Entwicklung. Als Fullstack-Entwickler berichtet unser Autor Jannik an...
Tags: Software, Technology

Von der Einführung der elektronischen Patientenakte bis zur Videosprechstunde – Das Voranschreiten der Digitalisierung im...
Tags: Infrastructure, Innovation, Digital Business

Im ultimativen Infrastrukturvergleich treten zwei unterschiedliche Plattformansätze einer...
Tags: Infrastructure, Technology

Beim Entwurf einer Microservice-Architektur für eine konkrete Anwendung müssen viele Entscheidungen getroffen werden, z.B....
Tags: Architecture

People need their phones to be productive – but phones have their limits“ – mit diesen Worten stellte der damalige Chief Product...
Tags: Software, Technology, Innovation

Irgendwann kommt der Zeitpunkt, an dem die Anwender der Software beginnen in den Begriffen des Modells zu denken und in diesem...
Tags: Software

Serverless eröffnet riesige Potenziale für die Frontend-Entwicklung. Als Fullstack-Entwickler berichtet unser Autor Jannik an...
Tags: Software, Technology

Power-Up für Ihre DevOps Organisation: Unsere DevOps-Experten präsentieren an dieser Stelle regelmäßig hilfreiche Praxistipps und...
Tags: Infrastructure, Technology, Innovation

Im ultimativen Infrastrukturvergleich treten zwei unterschiedliche Plattformansätze einer...
Tags: Infrastructure, Technology

Tags: Infrastructure, Technology

Im ultimativen Infrastrukturvergleich treten zwei unterschiedliche Plattformansätze einer...
Tags: Infrastructure, Technology

Non-fungible Token (NFTs) mischen gerade den Kunstmarkt auf und gehören zu den wichtigsten Trends in der Blockchain-Welt – Doch...
Tags: Innovation, Blockchain

Der Schlüssel zu einer neuen Form der Schmerztherapie liegt in der kontinuierlichen Überwachung des Blutdrucks. Aber gängige...
Tags: Software, Innovation

Analphabetismus ist eine gesellschaftliche Herausforderung. Eine App zur Leseförderung soll Menschen dabei helfen, ihre...
Tags: Software, Innovation

Im ultimativen Infrastrukturvergleich treten zwei unterschiedliche Plattformansätze einer...
Tags: Infrastructure, Technology

Im ultimativen Infrastrukturvergleich treten zwei unterschiedliche Plattformansätze einer...
Tags: Infrastructure, Technology

Wenig Zeit, steigende Paketzahlen und hohe Wettbewerbsintensität – Im umkämpften Markt der privaten Paketzustellung steigt der...
Tags: Technology, Innovation, Digital Business

Je komplexer Software-Entwicklungsprojekte sind, desto wichtiger ist ein agiles Vorgehensmodell, bei dem Anforderungen flexibel...
Tags: Agility, Digital Business

Im ultimativen Infrastrukturvergleich treten zwei unterschiedliche Plattformansätze einer...
Tags: Infrastructure, Technology

Eine im iteratec SLAB entwickelte, gemeinnützige Anwendung hilft Menschen mit Flucht- und Migrationshintergrund dabei,...
Tags: Software

Tags: Infrastructure, Technology

2020 hat uns gezeigt, wie eine Pandemie eingespielte Prozesse und sichergeglaubte Annahmen erschüttern kann. Damit meine ich...
Tags: Technology, Blockchain

Eine Augmented-Reality-Brille kann Pflegekräfte stärken und somit auch zu einem besseren Pflegeangebot führen. Das ist die Vision...
Tags: Software, Technology, Innovation

Einen großen Tanker...
Tags: Technology

Tags: Blockchain

Als Ende 2022 die neue Version von ChatGPT veröffentlicht wurde, überschlugen sich die Medien erneut und berichteten wahlweise...

In dieser Blogserie geben wir einen tieferen Einblick in die Themen IOTA und Hashgraph und die...
Tags: Technology, Blockchain

In diese Blogserie geben wir einen tieferen Einblick zu den Themen IOTA und Hashgraph...
Tags: Technology, Blockchain

Tags: Technology, Blockchain

Täglich 4.5 Milliarden „Likes“, über eine Milliarde Logins, 1.65 Milliarden aktive Nutzer - das sind Zahlen, die für das...
Tags: Software, Technology

In dieser Blogserie gehen wir näher auf Blockchain ein und widmen uns dabei verschiedenen...
Tags: Blockchain

Verteilte Systeme dominieren seit Jahrzehnten die Software-Welt....
Tags: Technology, Blockchain

In diese Blogserie geben wir einen tieferen Einblick in die Themen IOTA und Hashgraph und die dahinter liegenden Konzepte:
Tags: Technology, Blockchain

In dieser Blogserie gehen wir näher auf Blockchain ein und widmen uns dabei verschiedenen Fragestellungen:
Tags: Technology, Blockchain

In dieser Blogserie geben wir einen tieferen Einblick in die Themen IOTA und Hashgraph und die dahinter...
Tags: Technology, Blockchain

Alle reden über Scrum. Viele sagen, sie machen Scrum, vielleicht auch du! Aber machst du es auch richtig? Darfst du dein...
Tags: Agility

Nur wenige Begriffe werden so inflationär und schwammig benutzt wie Digitalisierung. Der Begriff Innovation kann allerdings...
Tags: Innovation
Vergangenen Sommer fragte sich Stefan Blum, ob wir durch Machine Learning nicht mehr...

Wer sich heute mit Innovationsmanagement befasst, kommt nicht um den Begriff der Open Innovation herum. Die Öffnung des...
Tags: Innovation

Am 26. März hat das 11. Scrum Meetup in Wien stattgefunden. Diesmal stand ein Spiel auf dem Programm. Es ging um...
Tags: Agility

„Agil heißt doch einfach nur schneller“ – dieser ernst gemeinte Beitrag in einer Diskussion zur grundsätzlichen Vorgehensweise...
Tags: Agility

Zuerst erschienen in Java Aktuell 03/2020 (ijug.eu)
Oft macht das Aufrufen von Webseiten und die Benutzung von komplexeren...
Tags: Software, Technology

Vor anderthalb Jahren, im Herbst 2018 erreichte uns die Anfrage eines möglichen Neukunden, der einen bekannten Webshop betreibt....
Tags: Technology, Agility

In dieser Blogserie gehen wir näher auf Elasticsearch ein und widmen uns dabei verschiedenen...
Tags: Software, Technology

Ich bin gelegentlich als Auditor für Softwareentwicklungs-Projekte unterwegs. Wenn ich agile Projekte reviewe, dann finde ich...
Tags: Software, Technology

Die Blog-Serie.
Im ersten Teil der Blog-Serie sind wir auf Unsupervised und Supervised Machine Learning...

Wir erinnern uns: In Teil 1 haben einen (mehr oder weniger) smarten Contract namens "Weisenheimer" in die Ethereum...
Tags: Technology, Blockchain

In dieser Blogserie gehen wir näher auf Elasticsearch ein und widmen uns dabei verschiedenen Fragestellungen:
Folgende...
Tags: Software, Technology

Wer nach den Begriffen Agile, Lean, Scrum oder UX sucht, findet viel Ärger und Frustration. Designer beklagen das Opfern der...
Tags: Technology, Agility

In Teil 1haben wir mit möglichst einfachen Mitteln den Smart Contract "Weisenheimer" in Rinkeby, einem Ethereum Test Network, ...
Tags: Technology, Blockchain